9597. Photoshoot

Farmer John is arranging his n cows numbered 1 ... n for a photoshoot. Initially, FJ planned for the i-th cow from the left to be the cow numbered a_i, and wrote down the permutation a₁, a₂, ..., a_n on a sheet of paper. Unfortunately, that paper was recently stolen by Farmer Nhoj!

Fortunately, there might still be a chance for FJ to recover the permutation that he originally wrote down. Before the sheet was stolen, Bessie recorded the sequence b₁, b₂, ..., b_n_-1, which satisfies b_i = a_i + a_i₊₁ for each i (1 ≤ i < n).

Based on Bessie’s information, help FJ restore the “lexicographically minimum” permutation a, which could lead to the sequence b. A permutation x is lexicographically smaller than a permutation y if for some j, x_i = y_i for all i < j and x_j < y_j (in other words, the two permutations are identical up to a certain point, at which x is smaller than y). It is guaranteed that at least one such a exists.

Input. The first line contains a single integer n (2 ≤ n ≤ 10³). The second line contains n – 1 integers b₁, b₂, ..., b_n_-1.

Output. Print the lexicographically minimum permutation a₁, a₂, ..., a_n .

Sample input

Sample output

4 6 7 6

3 1 5 2 4

SOLUTION

full search

Algorithm analysis

The number a₁ can range from 1 to n. Given a fixed value of a₁, the remaining numbers in the sequence a₂, ..., a_n are uniquely determined. Iterate a₁ from 1 to n, restore the sequence a and verify whether it constitutes a permutation of numbers from 1 to n (all a_i must be distinct and fall within the range from 1 to n). Once the reconstructed sequence a forms a permutation, print it and terminate the program.

Since b_i = a_i + a_i₊₁, then a_i₊₁ = b_i – a_i or a_i = b_i_-1 – a_i_-1.

Example

Let a₁ = 3. Then sequence b = (4, 6, 7, 6) generates the following sequence а:

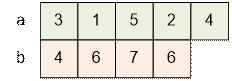
The sequence a = (3, 1, 5, 2, 4) is a permutation. The following relationship holds: 3 + 1 = 4, 1 + 5 = 6, 5 + 2 = 7, and 2 + 4 = 6.

If, for example, we choose a₁ = 1, then the following sequence а will be restored from the input sequence b = (4, 6, 7, 6):

The sequence a = (1, 3, 3, 4, 2) is not a permutation.

Algorithm realization

Declare the arrays. The array used will be used to verify whether a is a permutation.

#define MAX 1001

int a[MAX], b[MAX], used[MAX];

Read the input data.

scanf("%d", &n);

for (i = 0; i < n - 1; i++)

scanf("%d", &b[i]);

Iterate over the value of a₀ from 1 to n.

for (a0 = 1; a0 <= n; a0++)

{

a[0] = a0;

Compute the elements of the sequence a using the formula a_i = b_i_-1 – a_i_-1.

for (i = 1; i < n; i++)

a[i] = b[i - 1] - a[i - 1];

Initialize the array used with zeroes.

for (i = 1; i <= n; i++) used[i] = 0;

Check if a is a permutation. Each value of a_i must appear in the sequence only once and be within the range from 1 to n. The variable flag will be set to 1 if the sequence a is not a permutation.

flag = 0;

for (i = 0; i < n; i++)

{

if (a[i] < 1 || a[i] > n || used[a[i]])

{

flag = 1;

break;

}

used[a[i]] = 1;

}

If the sequence a is a permutation, print it and terminate the program.

if (flag == 0)

{

for (i = 0; i < n; i++)

printf("%d ", a[i]);

printf("\n");

return 0;

}

Python realization

Read the input data.

n = int(input())

b = list(map(int, input().split()))

Declare the lists. The list used will be used to check if a is a permutation.

a = [0] * n

used = [0] * (n + 1)

Iterate over the value of a₀ from 1 to n.

for a0 in range(1, n + 1):

a[0] = a0

Compute the elements of the sequence a using the formula a_i = b_i_-1 – a_i_-1.

for i in range(1, n):

a[i] = b[i - 1] - a[i - 1]

Initialize the list used with zeroes.

for i in range(1, n + 1):

used[i] = 0

flag = 0

for i in range(n):

if a[i] < 1 or a[i] > n or used[a[i]]:

flag = 1

break

used[a[i]] = 1

If the sequence a is a permutation, print it and terminate the program.

if flag == 0:

print(*a)

break